#include <gmc.h>
Inheritance diagram for LaGenMatComplex:
This is the basic LAPACK++ complex-valued matrix. It is a dense (nonsingular) matrix, assumes no special structure or properties.
Multiplication of this matrix should be done by the functions in blas1pp.h, blas2pp.h and blas3pp.h, e.g. Blas_Mat_Mat_Mult(). (There are also some operators in blaspp.h, but we advice against them because they will always allocate a new matrix for the result even though you usually already have a matrix at hand for writing the result into.) Transpositions of matrices usually do not have to be calculated explicitly, but you can directly use the different multiplication functions that will use a matrix as a transposed one, e.g. Blas_Mat_Trans_Mat_Mult().
To switch on the support for complex-valued matrices, you need to define the macro LA_COMPLEX_SUPPORT in your application before including the Lapack++ header files.
| typedef COMPLEX LaGenMatComplex::value_type |
The type of the value elements.
Convenience typedef of this class to itself to make common function definitions easier. (New in lapackpp-2.4.5)
| typedef VectorComplex LaGenMatComplex::vec_type |
Internal wrapper type; don't use that in an application.
| LaGenMatComplex::LaGenMatComplex | ( | ) |
Constructs a null 0x0 matrix.
| LaGenMatComplex::LaGenMatComplex | ( | int | m, | |
| int | n | |||
| ) |
Constructs a column-major matrix of size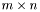 
. Matrix elements are NOT initialized!
| LaGenMatComplex::LaGenMatComplex | ( | COMPLEX * | v, | |
| int | m, | |||
| int | n, | |||
| bool | row_ordering = false | |||
| ) |
Constructs an 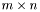matrix by using the values from the one-dimensional C array v of length m*n.
row_ordering is false, then the data will not be copied but instead the C array will be shared (shallow copy). In that case, you must not delete the C array as long as you use this newly created matrix. Also, if you need a copy (deep copy), construct one matrix A by this constructor, and then copy this content into a second matrix by B.copy(A). On the other hand, if row_ordering is true, then the data will be copied immediately (deep copy).| v | The one-dimensional C array of size m*n whose data should be used. If row_ordering is false, then the data will not be copied but shared (shallow copy). If row_ordering is true, then the data will be copied (deep copy). | |
| m | The number of rows in the new matrix. | |
| n | The number of columns in the new matrix. | |
| row_ordering | If false, then the C array is used in column-order, i.e. the first m elements of v are used as the first column of the matrix, the next m elements are the second column and so on. (This is the default and this is also the internal storage format in order to be compatible with the underlying Fortran subroutines.) If this is true, then the C array is used in row-order, i.e. the first n elements of v are used as the first row of the matrix, the next n elements are the second row and so on. (Internally, this is achieved by allocating a new copy of the array and copying the array into the internal ordering.) |
| LaGenMatComplex::LaGenMatComplex | ( | const LaGenMatComplex & | ) |
Create a new matrix from an existing one by copying.
Watch out! Due to the C++ "named return value optimization" you cannot use this as an alias for copy() when declaring a variable if the right-side is a return value of operator(). More precisely, you cannot write the following:
LaGenMatComplex x( y(LaIndex(),LaIndex()) ); // erroneous reference copy!
Instead, if the initialization should create a new copy of the right-side matrix, you have to write it this way:
LaGenMatComplex x( y(LaIndex(),LaIndex()).copy() ); // correct deep-copy
Or this way:
LaGenMatComplex x;
x = y(LaIndex(),LaIndex()); // correct deep-copy
| LaGenMatComplex::LaGenMatComplex | ( | const LaGenMatDouble & | s_real, | |
| const LaGenMatDouble & | s_imag = LaGenMatDouble() | |||
| ) | [explicit] |
Create a new matrix from a separate real and imaginary part. Uses s_real as real part and s_imag as imaginary part. If s_imag is not given, an imaginary part of zero is used.
| virtual LaGenMatComplex::~LaGenMatComplex | ( | ) | [virtual] |
Destroy matrix and reclaim vector memory space if this is the only structure using it.
| LaGenMatComplex& LaGenMatComplex::resize | ( | int | m, | |
| int | n | |||
| ) |
Resize to a new matrix of size m x n. The element values of the new matrix are uninitialized, even if resizing to a smaller matrix.
| LaGenMatComplex& LaGenMatComplex::resize | ( | const LaGenMatComplex & | s | ) |
Resize to a new matrix of the same size as the given matrix s. The element values of the new matrix are uninitialized, even if resizing to a smaller matrix.
| bool LaGenMatComplex::is_zero | ( | ) | const |
Returns true if this is an all-zero matrix. (New in lapackpp-2.4.5)
| bool LaGenMatComplex::is_submatrixview | ( | ) | const [inline] |
Returns true if this matrix is only a submatrix view of another (larger) matrix. (New in lapackpp-2.4.4)
| bool LaGenMatComplex::has_unitstride | ( | ) | const [inline] |
Returns true if this matrix has unit stride.
This is a necessary condition for not being a submatrix view, but it's not sufficient. (New in lapackpp-2.4.4)
| bool LaGenMatComplex::equal_to | ( | const LaGenMatComplex & | mat | ) | const |
Returns true if the given matrix mat is exactly equal to this object. (New in lapackpp-2.4.5)
| int LaGenMatComplex::size | ( | int | d | ) | const [inline] |
Returns the length n of the dth dimension, i.e. for a M x N matrix, size(0) returns M and size(1) returns N.
| int LaGenMatComplex::cols | ( | ) | const [inline] |
Returns the number of columns, i.e. for a M x N matrix this returns N. New in lapackpp-2.4.4.
| int LaGenMatComplex::rows | ( | ) | const [inline] |
Returns the number of rows, i.e. for a M x N matrix this returns M. New in lapackpp-2.4.4.
| int LaGenMatComplex::inc | ( | int | d | ) | const [inline] |
Returns the distance between memory locations (in terms of number of elements) between consecutive elements along dimension d. For example, if inc(d) returns 1, then elements along the dth dimension are contiguous in memory.
| int LaGenMatComplex::gdim | ( | int | d | ) | const [inline] |
Returns the global dimensions of the (possibly larger) matrix owning this space. This will only differ from size(d) if the current matrix is actually a submatrix view of some larger matrix.
| int LaGenMatComplex::start | ( | int | d | ) | const [inline] |
If the memory space used by this matrix is viewed as a linear array, start(d) returns the starting offset of the first element in dimension d. (See LaIndex class.)
| int LaGenMatComplex::end | ( | int | d | ) | const [inline] |
If the memory space used by this matrix is viewed as a linear array, end(d) returns the starting offset of the last element in dimension d. (See LaIndex class.)
| LaIndex LaGenMatComplex::index | ( | int | d | ) | const [inline] |
Returns the index specifying this submatrix view in dimension d. (See LaIndex class.) This will only differ from a unit-stride index if the current matrix is actually a submatrix view of some larger matrix.
| int LaGenMatComplex::ref_count | ( | ) | const [inline] |
Returns the number of data objects which utilize the same (or portions of the same) memory space used by this matrix.
| COMPLEX * LaGenMatComplex::addr | ( | ) | const [inline] |
Returns the memory address of the first element of the matrix. G.addr() is equivalent to &G(0,0) .
| COMPLEX & LaGenMatComplex::operator() | ( | int | i, | |
| int | j | |||
| ) | [inline] |
Returns the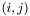 
th element of this matrix, with the indices i and j starting at zero (zero-based offset). This means you have
![\[ A_{n\times m} = \left(\begin{array}{ccc} a_{11} & & a_{1m} \\ & \ddots & \\ a_{n1} & & a_{nm} \end{array}\right) \]](form_18.png)
but for accessing the element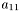 
you have to write A(0,0).
Optional runtime bounds checking (0<=i<m, 0<=j<n) is set by the compile time macro LA_BOUNDS_CHECK.
| COMPLEX & LaGenMatComplex::operator() | ( | int | i, | |
| int | j | |||
| ) | const [inline] |
Returns the th element of this matrix, with the indices i and j starting at zero (zero-based offset). This means you have
but for accessing the element 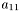you have to write A(0,0).
Optional runtime bounds checking (0<=i<m, 0<=j<n) is set by the compile time macro LA_BOUNDS_CHECK.
| LaGenMatComplex LaGenMatComplex::operator() | ( | const LaIndex & | I, | |
| const LaIndex & | J | |||
| ) |
Return a submatrix view specified by the indices I and J. (See LaIndex class.) These indices specify start, increment, and ending offsets, similar to triplet notation of Matlab or Fortran 90. For example, if B is a 10 x 10 matrix, I is (0:2:2) and J is (3:1:4), then B(I,J) denotes the 2 x 2 matrix
![\[ \left(\begin{array}{cc} b_{0,3} & b_{2,3} \\ b_{0,4} & b_{4,4} \end{array}\right) \]](form_20.png)
| LaGenMatComplex LaGenMatComplex::operator() | ( | const LaIndex & | I, | |
| const LaIndex & | J | |||
| ) | const |
Return a submatrix view specified by the indices I and J. (See LaIndex class.) These indices specify start, increment, and ending offsets, similar to triplet notation of Matlab or Fortran 90. For example, if B is a 10 x 10 matrix, I is (0:2:2) and J is (3:1:4), then B(I,J) denotes the 2 x 2 matrix
| LaGenMatComplex LaGenMatComplex::row | ( | int | k | ) |
Returns a submatrix view for the specified row k of this matrix.
The returned object references still the same memory as this object, so if you modify elements, they will appear modified in both objects. (New in lapackpp-2.4.6)
| LaGenMatComplex LaGenMatComplex::row | ( | int | k | ) | const |
Returns a submatrix view for the specified row k of this matrix.
The returned object references still the same memory as this object, so if you modify elements, they will appear modified in both objects. (New in lapackpp-2.4.6)
| LaGenMatComplex LaGenMatComplex::col | ( | int | k | ) |
Returns a submatrix view for the specified column k of this matrix.
The returned object references still the same memory as this object, so if you modify elements, they will appear modified in both objects. (New in lapackpp-2.4.6)
| LaGenMatComplex LaGenMatComplex::col | ( | int | k | ) | const |
Returns a submatrix view for the specified column k of this matrix.
The returned object references still the same memory as this object, so if you modify elements, they will appear modified in both objects. (New in lapackpp-2.4.6)
| LaGenMatComplex& LaGenMatComplex::operator= | ( | COMPLEX | s | ) |
Set elements of left-hand size to the scalar value s. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected.
Reimplemented in LaVectorComplex.
| LaGenMatComplex& LaGenMatComplex::operator= | ( | const LaComplex & | s | ) |
Set elements of left-hand size to the scalar value s. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected.
| LaGenMatComplex& LaGenMatComplex::operator= | ( | const LaGenMatComplex & | s | ) |
Release left-hand side (reclaiming memory space if possible) and copy elements of elements of s. Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.
This is an alias for copy().
Watch out! Due to the C++ "named return value optimization" you cannot use this as an alias for copy() when declaring a variable if the right-side is a return value of operator(). More precisely, you cannot write the following:
LaGenMatComplex x = y(LaIndex(),LaIndex()); // erroneous reference copy!
Instead, if the initialization should create a new copy of the right-side matrix, you have to write it this way:
LaGenMatComplex x = y(LaIndex(),LaIndex()).copy(); // correct deep-copy
Or this way:
LaGenMatComplex x;
x = y(LaIndex(),LaIndex()); // correct deep-copy
Note: The manual for lapack++-1.1 claimed that this operator would be an alias for ref(), not for copy(), i.e. this operator creates a reference instead of a deep copy. However, since that confused many people, the behaviour was changed so that B=A will now create B as a deep copy instead of a reference. If you want a reference, please write B.ref(A) explicitly.
Reimplemented in LaVectorComplex.
| LaGenMatComplex& LaGenMatComplex::operator+= | ( | COMPLEX | s | ) |
Add the scalar value s to elements of left-hand side. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected.
| LaGenMatComplex& LaGenMatComplex::add | ( | COMPLEX | s | ) |
Add the scalar value s to elements of left-hand side. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected. (New in lapackpp-2.4.7.)
| LaGenMatComplex& LaGenMatComplex::scale | ( | const LaComplex & | s | ) |
Scale the left-hand side matrix by the given scalar value. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected. (New in lapackpp-2.4.7.)
| LaGenMatComplex& LaGenMatComplex::scale | ( | COMPLEX | s | ) |
Scale the left-hand side matrix by the given scalar value. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected. (New in lapackpp-2.4.7.)
| LaGenMatComplex& LaGenMatComplex::operator *= | ( | COMPLEX | s | ) |
Scale the left-hand side matrix by the given scalar value. No new matrix is created, so that if there are other matrices that reference this memory space, they will also be affected. (New in lapackpp-2.4.7.)
| LaGenMatComplex& LaGenMatComplex::inject | ( | const LaGenMatComplex & | s | ) |
Copy elements of s into the memory space referenced by the left-hand side, without first releasing it. The effect is that if other matrices share memory with left-hand side, they too will be affected. Note that the size of s must be the same as that of the left-hand side matrix.
s, you should use copy() instead. Reimplemented in LaVectorComplex.
| LaGenMatComplex& LaGenMatComplex::copy | ( | const LaGenMatComplex & | s | ) |
Release left-hand side (reclaiming memory space if possible) and copy elements of elements of s. Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.
Reimplemented in LaVectorComplex.
| LaGenMatComplex LaGenMatComplex::copy | ( | ) | const |
Returns a newly allocated matrix that is an element-by-element copy of this matrix.
New in lapackpp-2.5.2
| LaGenMatComplex& LaGenMatComplex::copy | ( | const LaGenMatDouble & | s_real, | |
| const LaGenMatDouble & | s_imag = LaGenMatDouble() | |||
| ) |
Release left-hand side (reclaiming memory space if possible) and copy elements of s_real as real part and s_imag as imaginary part into the left-hand side. If s_imag is not given, an imaginary part of zero is used.
Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.
| LaGenMatComplex & LaGenMatComplex::shallow_assign | ( | ) | [inline] |
This is an optimization for returning temporary matrices from functions, without copying. The shallow_assign() function essentially sets an internal flag which instructs the X::X(&X) copy constructor to avoid the copying.
| LaGenMatComplex& LaGenMatComplex::ref | ( | const LaGenMatComplex & | s | ) |
Let this matrix reference the given matrix s, so that the given matrix memory s is now referenced by multiple objects (by the given object s and now also by this object). Handle this with care!
This function releases any previously referenced memory of this object.
Reimplemented in LaVectorComplex.
| LaGenMatComplex LaGenMatComplex::repmat | ( | int | M, | |
| int | N | |||
| ) | const |
Returns a newly allocated large matrix that consists of M-by-N copies of the given matrix. (New in lapackpp-2.4.5.)
| value_type LaGenMatComplex::trace | ( | ) | const |
Returns the trace, i.e. the sum of all diagonal elements of the matrix. (New in lapackpp-2.4.5)
| LaGenMatComplex LaGenMatComplex::diag | ( | ) | const |
Returns a newly allocated column vector of dimension Nx1 that contains the diagonal of the given matrix. (New in lapackpp-2.4.5)
| LaGenMatDouble LaGenMatComplex::real | ( | ) | const |
Returns a newly allocated matrix with the real part of this matrix as a double (floating-point double precision) matrix. An alias for real_to_LaGenMatDouble(). (New in lapackpp-2.4.5)
| LaGenMatDouble LaGenMatComplex::imag | ( | ) | const |
Returns a newly allocated matrix with the imaginary part of this matrix as a double (floating-point double precision) matrix. An alias for imag_to_LaGenMatDouble(). (New in lapackpp-2.4.5)
| int LaGenMatComplex::shallow | ( | ) | const [inline] |
Returns global shallow flag
| int LaGenMatComplex::debug | ( | ) | const [inline] |
Returns global debug flag
| int LaGenMatComplex::debug | ( | int | d | ) | [inline] |
Set global debug flag
| const LaGenMatComplex& LaGenMatComplex::info | ( | ) | const [inline] |
use as in
std::cout << B.info() << std::endl;
this *info_ member is unique in that it really isn't part of the matrix info, just a flag as to how to print it. We've included in this beta release as part of our testing, but we do not expect it to be user accessable.
| std::ostream& LaGenMatComplex::Info | ( | std::ostream & | s | ) | const [inline] |
Print the matrix info (not the actual elements) to the given ostream.
| LaGenMatDouble LaGenMatComplex::real_to_LaGenMatDouble | ( | ) | const |
Convert the real part of this matrix to a double (floating-point double precision) matrix.
| LaGenMatFloat LaGenMatComplex::real_to_LaGenMatFloat | ( | ) | const |
Convert the real part of this matrix to a float (floating-point single precision) matrix.
| LaGenMatInt LaGenMatComplex::real_to_LaGenMatInt | ( | ) | const |
Convert the real part of this matrix to an int matrix.
| LaGenMatLongInt LaGenMatComplex::real_to_LaGenMatLongInt | ( | ) | const |
Convert the real part of this matrix to a long int matrix.
| LaGenMatDouble LaGenMatComplex::imag_to_LaGenMatDouble | ( | ) | const |
Convert the imaginary part of this matrix to a double (floating-point double precision) matrix.
| LaGenMatFloat LaGenMatComplex::imag_to_LaGenMatFloat | ( | ) | const |
Convert the imaginary part of this matrix to a float (floating-point single precision) matrix.
| LaGenMatInt LaGenMatComplex::imag_to_LaGenMatInt | ( | ) | const |
Convert the imaginary part of this matrix to an int matrix.
| LaGenMatLongInt LaGenMatComplex::imag_to_LaGenMatLongInt | ( | ) | const |
Convert the imaginary part of this matrix to a long int matrix.
| static LaGenMatComplex LaGenMatComplex::zeros | ( | int | N, | |
| int | M = 0 | |||
| ) | [static] |
Returns a newly allocated all-zero matrix of dimension NxN, if M is not given, or NxM if M is given. (New in lapackpp-2.4.5)
| static LaGenMatComplex LaGenMatComplex::ones | ( | int | N, | |
| int | M = 0 | |||
| ) | [static] |
Returns a newly allocated all-one matrix of dimension NxN, if M is not given, or NxM if M is given. (New in lapackpp-2.4.5)
| static LaGenMatComplex LaGenMatComplex::eye | ( | int | N, | |
| int | M = 0 | |||
| ) | [static] |
Returns a newly allocated identity matrix of dimension NxN, if M is not given, or a rectangular matrix NxM if M is given. (New in lapackpp-2.4.5)
| static LaGenMatComplex LaGenMatComplex::rand | ( | int | N, | |
| int | M, | |||
| double | low = 0, |
|||
| double | high = 1 | |||
| ) | [static] |
Returns a newly allocated matrix of dimension NxM with pseudo-random values. Both real part and imaginary part values are uniformly distributed in the interval (0,1) or, if specified, (low,high). (New in lapackpp-2.4.5)
Note: Since this uses the system's rand() call, the randomness of the values might be questionable -- don't use this if you need really strong random numbers.
| static LaGenMatComplex LaGenMatComplex::from_diag | ( | const LaGenMatComplex & | vect | ) | [static] |
Returns a newly allocated diagonal matrix of dimension NxN that has the vector vect of length N on the diagonal. (New in lapackpp-2.4.5)
| static LaGenMatComplex LaGenMatComplex::linspace | ( | value_type | start, | |
| value_type | end, | |||
| int | nr_points | |||
| ) | [static] |
Returns a newly allocated linarly spaced column vector with nr_points elements, between and including start and end. (New in lapackpp-2.4.5.)
| std::ostream& operator<< | ( | std::ostream & | , | |
| const LaGenMatComplex & | ||||
| ) | [friend] |
Print the matrix to the given output stream. If the matrix info flag is set, then this prints only the matrix info, see LaGenMatDouble::info(). Otherwise all matrix elements are printed.
1.5.0