|
Real-valued general matrices |
| void | Blas_Mat_Mat_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaGenMatDouble &C, bool transpose_A, bool transpose_B=false, double alpha=1.0, double beta=0.0) |
| void | Blas_Mat_Mat_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaGenMatDouble &C, double alpha=1.0, double beta=0.0) |
| void | Blas_Mat_Trans_Mat_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaGenMatDouble &C, double alpha=1.0, double beta=0.0) |
| void | Blas_Mat_Mat_Trans_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaGenMatDouble &C, double alpha=1.0, double beta=0.0) |
| void | Blas_Mat_Mat_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaVectorDouble &C) |
| void | Blas_Mat_Trans_Mat_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaVectorDouble &C) |
| void | Blas_Mat_Mat_Trans_Mult (const LaGenMatDouble &A, const LaGenMatDouble &B, LaVectorDouble &C) |
| void | Blas_Scale (double s, LaGenMatDouble &A) |
Complex-valued matrices |
| void | Blas_Mat_Mat_Mult (const LaGenMatComplex &A, const LaGenMatComplex &B, LaGenMatComplex &C, bool hermit_A, bool hermit_B=false, LaComplex alpha=1.0, LaComplex beta=0.0) |
| void | Blas_Mat_Mat_Mult (const LaGenMatComplex &A, const LaGenMatComplex &B, LaGenMatComplex &C, LaComplex alpha=1.0, LaComplex beta=0.0) |
| void | Blas_Mat_Trans_Mat_Mult (const LaGenMatComplex &A, const LaGenMatComplex &B, LaGenMatComplex &C, LaComplex alpha=1.0, LaComplex beta=0.0) |
| void | Blas_Mat_Mat_Trans_Mult (const LaGenMatComplex &A, const LaGenMatComplex &B, LaGenMatComplex &C, LaComplex alpha=1.0, LaComplex beta=0.0) |
| void | Blas_Scale (COMPLEX s, LaGenMatComplex &A) |
Symmetric matrices |
| void | Blas_Mat_Mat_Mult (LaSymmMatDouble &A, LaGenMatDouble &B, LaGenMatDouble &C, double alpha=1.0, double beta=1.0, bool b_left_side=true) |
| void | Blas_R1_Update (LaSymmMatDouble &C, LaGenMatDouble &A, double alpha=1.0, double beta=1.0, bool right_transposed=true) |
| void | Blas_R2_Update (LaSymmMatDouble &C, LaGenMatDouble &A, LaGenMatDouble &B, double alpha=1.0, double beta=1.0, bool right_transposed=true) |
Matrix Norms |
| double | Blas_Norm1 (const LaGenMatDouble &A) |
| | 1-Norm: Maximum column sum
|
| double | Blas_Norm_Inf (const LaGenMatDouble &A) |
| | Infinity-Norm: Maximum row sum.
|
| double | Blas_NormF (const LaGenMatDouble &A) |
| | Frobenius-Norm.
|
| double | Blas_Norm1 (const LaGenMatComplex &A) |
| | 1-Norm: Maximum column sum
|
| double | Blas_Norm_Inf (const LaGenMatComplex &A) |
| | Infinity-Norm: Maximum row sum.
|
| double | Blas_NormF (const LaGenMatComplex &A) |
| | Frobenius-Norm.
|
| double | Norm_Inf (const LaBandMatDouble &A) |
| double | Norm_Inf (const LaSymmMatDouble &S) |
| double | Norm_Inf (const LaSpdMatDouble &S) |
| double | Norm_Inf (const LaSymmTridiagMatDouble &S) |
| double | Norm_Inf (const LaTridiagMatDouble &T) |
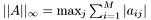 ,
,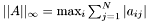 ,
,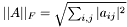 , i.e. the square root of the sum of the absolute squares of its elements.
, i.e. the square root of the sum of the absolute squares of its elements. 1.5.0
1.5.0