#include <lavc.h>
Inheritance diagram for LaVectorComplex:

Declaration | |
| LaVectorComplex () | |
| LaVectorComplex (int n) | |
| LaVectorComplex (int m, int n) | |
| LaVectorComplex (COMPLEX *v, int n) | |
| LaVectorComplex (COMPLEX *, int m, int n) | |
| LaVectorComplex (const LaGenMatComplex &) | |
Information | |
| int | size () const |
| int | inc () const |
| int | start () const |
| int | end () const |
| LaIndex | index () const |
Access functions | |
| COMPLEX & | operator() (int i) |
| const COMPLEX & | operator() (int i) const |
| LaVectorComplex | operator() (const LaIndex &i) |
| LaVectorComplex | operator() (const LaIndex &i) const |
Assignments | |
| LaVectorComplex & | operator= (COMPLEX s) |
| LaVectorComplex & | operator= (LaComplex s) |
| LaVectorComplex & | operator= (double s) |
| LaVectorComplex & | operator= (const LaGenMatComplex &s) |
| LaVectorComplex & | inject (const LaGenMatComplex &s) |
| LaVectorComplex & | copy (const LaGenMatComplex &s) |
| LaVectorComplex & | ref (const LaGenMatComplex &s) |
A vector is simply an nx1 or 1xn, matrix, only that it can be constructed and accessed by a single dimension.
Multiplication of this vector should be done by the functions in blas1pp.h and blas2pp.h, e.g. Blas_H_Dot_Prod() or Blas_Add_Mult(). (There are also some operators in blaspp.h, but we advice against them because they will always allocate a new matrix for the result even though you usually already have a matrix at hand for writing the result into.) Transpositions of vectors usually do not have to be calculated explicitly, but you can directly use the different multiplication functions that will use this vector as a transposed one, e.g. Blas_R1_Update().
| LaVectorComplex::LaVectorComplex | ( | ) | [inline] |
Constructs a column vector of length 0 (null).
| LaVectorComplex::LaVectorComplex | ( | int | n | ) | [inline] |
Constructs a column vector of length n
| LaVectorComplex::LaVectorComplex | ( | int | m, | |
| int | n | |||
| ) | [inline] |
Constructs a vector of size 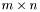 . One of the two dimensions must be one!
. One of the two dimensions must be one!
| LaVectorComplex::LaVectorComplex | ( | COMPLEX * | v, | |
| int | n | |||
| ) | [inline] |
Constructs a column vector of length n by copying the values from a one-dimensional C array of length n.
| LaVectorComplex::LaVectorComplex | ( | COMPLEX * | , | |
| int | m, | |||
| int | n | |||
| ) | [inline] |
Constructs an 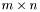 vector by copying the values from a one-dimensional C array of length mn. One of the two dimensions must be one!
vector by copying the values from a one-dimensional C array of length mn. One of the two dimensions must be one!
| LaVectorComplex::LaVectorComplex | ( | const LaGenMatComplex & | ) | [inline] |
Create a new vector from an existing matrix by copying. The given matrix s must be a vector, i.e. one of its dimensions must be one!
| int LaVectorComplex::size | ( | ) | const [inline] |
Returns the length n of this vector.
| int LaVectorComplex::inc | ( | ) | const [inline] |
Returns the distance between memory locations (in terms of number of elements) between consecutive elements along dimension d. For example, if inc(d) returns 1, then elements along the dth dimension are contiguous in memory.
| int LaVectorComplex::start | ( | ) | const [inline] |
If the memory space used by this matrix is viewed as a linear array, start(d) returns the starting offset of the first element in dimension d. (See LaIndex class.)
| int LaVectorComplex::end | ( | ) | const [inline] |
If the memory space used by this matrix is viewed as a linear array, end(d) returns the starting offset of the last element in dimension d. (See LaIndex class.)
| LaIndex LaVectorComplex::index | ( | ) | const [inline] |
Returns the index specifying this submatrix view in dimension d. (See LaIndex class.) This will only differ from a unit-stride index is the current matrix is actually a submatrix view of some larger matrix.
| COMPLEX & LaVectorComplex::operator() | ( | int | i | ) | [inline] |
Returns the  th element of this vector, with the index i starting at zero (zero-based offset). This means you have
th element of this vector, with the index i starting at zero (zero-based offset). This means you have
![\[ v = \left(\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_N \end{array}\right) \]](form_23.png)
but for accessing the element 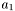 you have to write
you have to write v(0).
Optional runtime bounds checking (0<=i<=n) is set by the compile time macro LA_BOUNDS_CHECK.
| const COMPLEX & LaVectorComplex::operator() | ( | int | i | ) | const [inline] |
Returns the  th element of this vector, with the index i starting at zero (zero-based offset). This means you have
th element of this vector, with the index i starting at zero (zero-based offset). This means you have
![\[ v = \left(\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_N \end{array}\right) \]](form_23.png)
but for accessing the element 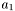 you have to write
you have to write v(0).
Optional runtime bounds checking (0<=i<=n) is set by the compile time macro LA_BOUNDS_CHECK.
| LaVectorComplex LaVectorComplex::operator() | ( | const LaIndex & | i | ) | [inline] |
Return a submatrix view specified by the index I. (See LaIndex class.) These indices specify start, increment, and ending offsets, similar to triplet notation of Matlab or Fortran 90. For example, if B is a 10 x 10 matrix, I is (0:2:2) and J is (3:1:4), then B(I,J) denotes the 2 x 2 matrix
![\[ \left(\begin{array}{cc} b_{0,3} & b_{2,3} \\ b_{0,4} & b_{4,4} \end{array}\right) \]](form_20.png)
| LaVectorComplex LaVectorComplex::operator() | ( | const LaIndex & | i | ) | const [inline] |
Return a submatrix view specified by the index I. (See LaIndex class.) These indices specify start, increment, and ending offsets, similar to triplet notation of Matlab or Fortran 90. For example, if B is a 10 x 10 matrix, I is (0:2:2) and J is (3:1:4), then B(I,J) denotes the 2 x 2 matrix
![\[ \left(\begin{array}{cc} b_{0,3} & b_{2,3} \\ b_{0,4} & b_{4,4} \end{array}\right) \]](form_20.png)
| LaVectorComplex & LaVectorComplex::operator= | ( | COMPLEX | s | ) | [inline] |
Set elements of left-hand size to the scalar value s. No new vector is created, so that if there are other vectors that reference this memory space, they will also be affected.
Reimplemented from LaGenMatComplex.
| LaVectorComplex & LaVectorComplex::operator= | ( | LaComplex | s | ) | [inline] |
Set elements of left-hand size to the scalar value s. No new vector is created, so that if there are other vectors that reference this memory space, they will also be affected.
| LaVectorComplex & LaVectorComplex::operator= | ( | double | s | ) | [inline] |
Set elements of left-hand size to the scalar value s. No new vector is created, so that if there are other vectors that reference this memory space, they will also be affected.
| LaVectorComplex & LaVectorComplex::operator= | ( | const LaGenMatComplex & | s | ) | [inline] |
Release left-hand side (reclaiming memory space if possible) and copy elements of elements of s. Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.
This is an alias for copy().
Reimplemented from LaGenMatComplex.
| LaVectorComplex & LaVectorComplex::inject | ( | const LaGenMatComplex & | s | ) | [inline] |
Copy elements of s into the memory space referenced by the left-hand side, without first releasing it. The effect is that if other vectors share memory with left-hand side, they too will be affected. Note that the size of s must be the same as that of the left-hand side vector.
s, you should use copy() instead. Reimplemented from LaGenMatComplex.
| LaVectorComplex & LaVectorComplex::copy | ( | const LaGenMatComplex & | s | ) | [inline] |
Release left-hand side (reclaiming memory space if possible) and copy elements of elements of s. Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.
Reimplemented from LaGenMatComplex.
| LaVectorComplex & LaVectorComplex::ref | ( | const LaGenMatComplex & | s | ) | [inline] |
Let this vector reference the given vector s, so that the given vector memory s is now referenced by multiple objects (by the given object s and now also by this object). Handle this with care!
This function releases any previously referenced memory of this object.
Reimplemented from LaGenMatComplex.
 1.5.0
1.5.0