| double Blas_Norm1 | ( | const LaVectorComplex & | dx | ) |
1-Norm
Returns the sum of the absolute values: 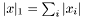
- See also:
- Eric W. Weisstein. "Vector Norm." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/VectorNorm.html
Go to the source code of this file.
Complex-valued vector operations | |
| void | Blas_Add_Mult (LaVectorComplex &dy, COMPLEX da, const LaVectorComplex &dx) |
| Combined vector scaling and addition (saxpy). | |
| void | Blas_Mult (LaVectorComplex &dy, COMPLEX da, const LaVectorComplex &dx) |
| Vector scaling. | |
| COMPLEX | Blas_U_Dot_Prod (const LaVectorComplex &cx, const LaVectorComplex &cy) |
| Non-conjugated dot product (very unusual!). | |
| COMPLEX | Blas_H_Dot_Prod (const LaVectorComplex &cx, const LaVectorComplex &cy) |
| Dot product. | |
| void | Blas_Copy (const LaVectorComplex &dx, LaVectorComplex &dy) |
| void | Blas_Scale (COMPLEX da, LaVectorComplex &dx) |
| void | Blas_Swap (LaVectorComplex &dx, LaVectorComplex &dy) |
Real-valued vector operations | |
| void | Blas_Add_Mult (LaVectorDouble &dy, double da, const LaVectorDouble &dx) |
| Combined vector scaling and addition (saxpy). | |
| void | Blas_Mult (LaVectorDouble &dy, double da, const LaVectorDouble &dx) |
| Vector scaling. | |
| double | Blas_Dot_Prod (const LaVectorDouble &dx, const LaVectorDouble &dy) |
| Dot product. | |
| void | Blas_Apply_Plane_Rot (LaVectorDouble &dx, LaVectorDouble &dy, double &c, double &s) |
| Apply Givens plane rotation. | |
| void | Blas_Gen_Plane_Rot (double &da, double &db, double &c, double &s) |
| Construct Givens plane rotation. | |
| void | Blas_Copy (const LaVectorDouble &dx, LaVectorDouble &dy) |
| void | Blas_Scale (double da, LaVectorDouble &dx) |
| void | Blas_Swap (LaVectorDouble &dx, LaVectorDouble &dy) |
Vector norms | |
| double | Blas_Norm1 (const LaVectorComplex &dx) |
| 1-Norm | |
| double | Blas_Norm2 (const LaVectorComplex &dx) |
| 2-Norm, Euclidean Norm | |
| int | Blas_Index_Max (const LaVectorComplex &dx) |
| double | Blas_Norm_Inf (const LaVectorComplex &x) |
| Infinity-Norm. | |
| double | Blas_Norm1 (const LaVectorDouble &dx) |
| 1-Norm | |
| double | Blas_Norm2 (const LaVectorDouble &dx) |
| 2-Norm, Euclidean Norm | |
| int | Blas_Index_Max (const LaVectorDouble &dx) |
| double | Blas_Norm_Inf (const LaVectorDouble &x) |
| Infinity-Norm. | |
This file defines the basic operations on vectors itself, commonly known as the Blas Level-1 routines.
| void Blas_Add_Mult | ( | LaVectorComplex & | dy, | |
| COMPLEX | da, | |||
| const LaVectorComplex & | dx | |||
| ) |
Combined vector scaling and addition (saxpy).
Combined vector scaling and addition: dy = dy + da * dx
| void Blas_Mult | ( | LaVectorComplex & | dy, | |
| COMPLEX | da, | |||
| const LaVectorComplex & | dx | |||
| ) |
Vector scaling.
Vector scaling: dy = da * dx
| COMPLEX Blas_U_Dot_Prod | ( | const LaVectorComplex & | cx, | |
| const LaVectorComplex & | cy | |||
| ) |
Non-conjugated dot product (very unusual!).
Returns the dot product of two vectors x and y, which is Sum(x[i]*y[i]), without taking any complex conjugate, which is a difference to the usual definition of complex dot products. This is probably not what you want, and you probably want to use Blas_H_Dot_Prod() instead.
x'*y . This function rather calculates (Matlab-notation) x.'*y . | COMPLEX Blas_H_Dot_Prod | ( | const LaVectorComplex & | cx, | |
| const LaVectorComplex & | cy | |||
| ) |
Dot product.
Returns the dot product of two vectors conj(x) and y, where the first vector is taken conjugate complex, which is Sum(conj(x[i])*y[i]). Note: This is not commutative any longer but rather complex conjugate commutative. But this is the usual case for these complex vectors.
| void Blas_Copy | ( | const LaVectorComplex & | dx, | |
| LaVectorComplex & | dy | |||
| ) |
Vector assignment (copying): dy = dx
| void Blas_Scale | ( | COMPLEX | da, | |
| LaVectorComplex & | dx | |||
| ) |
Vector scaling: dx = da * dx
| void Blas_Swap | ( | LaVectorComplex & | dx, | |
| LaVectorComplex & | dy | |||
| ) |
Swaps the elements of two vectors: dx <=> dy
| void Blas_Add_Mult | ( | LaVectorDouble & | dy, | |
| double | da, | |||
| const LaVectorDouble & | dx | |||
| ) |
Combined vector scaling and addition (saxpy).
Combined vector scaling and addition: dy = dy + da * dx
| void Blas_Mult | ( | LaVectorDouble & | dy, | |
| double | da, | |||
| const LaVectorDouble & | dx | |||
| ) |
Vector scaling.
Vector scaling: dy = da * dx
| double Blas_Dot_Prod | ( | const LaVectorDouble & | dx, | |
| const LaVectorDouble & | dy | |||
| ) |
Dot product.
Returns the dot product of two vectors x and y, which is Sum(x[i]*y[i]).
| void Blas_Apply_Plane_Rot | ( | LaVectorDouble & | dx, | |
| LaVectorDouble & | dy, | |||
| double & | c, | |||
| double & | s | |||
| ) |
Apply Givens plane rotation.
Applies a Givens plane rotation to (x,y): dx = c*dx + s*dy; dy = c*dy - s*dx
| void Blas_Gen_Plane_Rot | ( | double & | da, | |
| double & | db, | |||
| double & | c, | |||
| double & | s | |||
| ) |
Construct Givens plane rotation.
Construct a Givens plane rotation for (a,b). da, db are the rotational elimination parameters a,b.
| void Blas_Copy | ( | const LaVectorDouble & | dx, | |
| LaVectorDouble & | dy | |||
| ) |
Vector assignment (copying): dy = dx
| void Blas_Scale | ( | double | da, | |
| LaVectorDouble & | dx | |||
| ) |
Vector scaling: dx = da * dx
| void Blas_Swap | ( | LaVectorDouble & | dx, | |
| LaVectorDouble & | dy | |||
| ) |
Swaps the elements of two vectors: dx <=> dy
| double Blas_Norm1 | ( | const LaVectorComplex & | dx | ) |
1-Norm
Returns the sum of the absolute values: 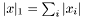
| double Blas_Norm2 | ( | const LaVectorComplex & | dx | ) |
2-Norm, Euclidean Norm
Returns the euclidean norm of the vector: 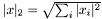
In other notation sqrt(conj(x')*x) or in Matlab notation sqrt(x'*x)
| int Blas_Index_Max | ( | const LaVectorComplex & | dx | ) |
Returns the index of largest absolute value; i such that |x[i]| == max(|x[0]|,|x[1]|,...)
| double Blas_Norm_Inf | ( | const LaVectorComplex & | x | ) | [inline] |
Infinity-Norm.
Returns the Infinity norm of a vector, which is the absolute value of its maximum element: 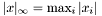
| double Blas_Norm1 | ( | const LaVectorDouble & | dx | ) |
1-Norm
Returns the sum of the absolute values: 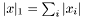
| double Blas_Norm2 | ( | const LaVectorDouble & | dx | ) |
2-Norm, Euclidean Norm
Returns the euclidean norm of the vector: 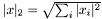
In other notation sqrt(conj(x')*x) or in Matlab notation sqrt(x'*x)
| int Blas_Index_Max | ( | const LaVectorDouble & | dx | ) |
Returns the index of largest absolute value; i such that |x[i]| == max(|x[0]|,|x[1]|,...)
| double Blas_Norm_Inf | ( | const LaVectorDouble & | x | ) | [inline] |
Infinity-Norm.
Returns the Infinity norm of a vector, which is the absolute value of its maximum element: 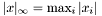
 1.5.0
1.5.0