LaTridiagMatDouble Class Reference

Tridiagonal square matrix class. More...

#include <trmd.h>

List of all members.

Declaration

 LaTridiagMatDouble ()
 LaTridiagMatDouble (int N)
 LaTridiagMatDouble (const LaTridiagMatDouble &)
 LaTridiagMatDouble (const LaVectorDouble &diag, const LaVectorDouble &diaglower, const LaVectorDouble &diagupper)
 ~LaTridiagMatDouble ()

Information

int size () const

Access functions

double & operator() (int i, int j)
double operator() (int i, int j) const
LaVectorDouble & diag (int diag_selection)
const LaVectorDouble & diag (int diag_selection) const

Assignments

LaTridiagMatDouble & copy (const LaTridiagMatDouble &s)
LaTridiagMatDouble & inject (const LaTridiagMatDouble &s)
LaTridiagMatDouble & ref (LaTridiagMatDouble &)

Debugging information

const LaTridiagMatDouble & info () const
int debug () const

Friends

std::ostream & operator<< (std::ostream &, const LaTridiagMatDouble &)

Detailed Description

Tridiagonal square matrix class.

Unlike general banded matrices, this tridiagonal matrix is stored by diagonals rather than columns. A tridiagonal matrix of order N is stored in three one-dimensional array, one of length N containing the diagonal elements and two of length N-1 containing the subdiagonal and superdiagonal elements with element index 0 through N-2.

One such matrix with the element indices looks as follows:

\[ A_{n\times n} = \left(\begin{array}{cccc} a_{00} & a_{01} & \cdots & 0 \\ a_{10} & \ddots & & \\ & & \ddots & a_{(n-2)(n-1)} \\ 0 & \cdots & a_{(n-1)(n-2)} & a_{(n-1)(n-1)} \end{array}\right) \]

Multiplication of this matrix should be done by the functions in blas1pp.h, blas2pp.h and blas3pp.h, e.g. Blas_Mat_Mat_Mult(), except that currently there isn't any function available for this class. Please ask on the lapackpp-devel mailing list for support if you need any assistance with this.

See also:
LaTridiagFactDouble, LaTridiagMatFactorize()

Constructor & Destructor Documentation

LaTridiagMatDouble::LaTridiagMatDouble (  ) 

Constructs a null 0x0 matrix.

LaTridiagMatDouble::LaTridiagMatDouble ( int  N  ) 

Constructs a tridiagonal matrix of size 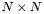$N\times N$. Matrix elements are NOT initialized!

LaTridiagMatDouble::LaTridiagMatDouble ( const LaTridiagMatDouble &   ) 

Create a new matrix from an existing one by copying (deep-copy).

LaTridiagMatDouble::LaTridiagMatDouble ( const LaVectorDouble &  diag,
const LaVectorDouble &  diaglower,
const LaVectorDouble &  diagupper 
)

Create a new matrix from the given three diagonals. The dimensions must match: diag must be of length N, diaglower and diagupper of dimension N-1, otherwise a failed assertion will terminate the program.

LaTridiagMatDouble::~LaTridiagMatDouble (  ) 

Destroy matrix and reclaim vector memory space if this is the only structure using it.

Member Function Documentation

int LaTridiagMatDouble::size (  )  const [inline]

Returns the size 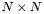$N\times N$ of this tridiagonal square matrix.

double & LaTridiagMatDouble::operator() ( int  i,
int  j 
) [inline]

Returns the 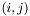$(i,j)$th element of this matrix, with the indices i and j starting at zero (zero-based offset). This means you have

\[ A_{n\times n} = \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & 0 \\ a_{21} & \ddots & & \\ & & \ddots & a_{(n-1)n} \\ 0 & \cdots & a_{n(n-1)} & a_{nn} \end{array}\right) \]

but for accessing the element 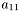$a_{11}$ you have to write A(0,0).

Optional runtime bounds checking (0<=i<m, 0<=j<n) is set by the compile time macro LA_BOUNDS_CHECK.

Note:
This operator was broken all the way until lapackpp-2.4.11 (regarding the lower diagonal) and is fixed since lapackpp-2.4.12.

double LaTridiagMatDouble::operator() ( int  i,
int  j 
) const [inline]

Returns the 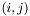$(i,j)$th element of this matrix, with the indices i and j starting at zero (zero-based offset). This means you have

\[ A_{n\times n} = \left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & 0 \\ a_{21} & \ddots & & \\ & & \ddots & a_{(n-1)n} \\ 0 & \cdots & a_{n(n-1)} & a_{nn} \end{array}\right) \]

but for accessing the element 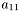$a_{11}$ you have to write A(0,0).

Optional runtime bounds checking (0<=i<m, 0<=j<n) is set by the compile time macro LA_BOUNDS_CHECK.

Note:
This operator was broken all the way until lapackpp-2.4.11 (regarding the lower diagonal) and is fixed since lapackpp-2.4.12.

LaVectorDouble& LaTridiagMatDouble::diag ( int  diag_selection  ) 

Returns the diagonal diag_selection: 0 main, -1 lower, 1 upper, 2 second upper.

(Actually, this class additionally stores the second upper diagonal of length N-2, selected by diag_selection==2, but this is only being used in LaTridiagMatFactorize().)

Note:
When assigning values or vectors to the returned diagonals, make sure you only use LaVectorDouble::inject instead of LaVectorDouble::copy or LaVectorDouble::operator=(). Please write this as follows: 
  LaVectorDouble newdiag(N);
  newdiag(0) = ...;
  LaTriagMatDouble triagmat(N);
  triagmat.diag(0).inject(newdiag); // correct
  // but don't write this:
  triagmat.diag(0) = newdiag; // wrong!
Watch out: You can directly manipulate the internal storage with this method! In particular, it would be possible to change the length of the returned vector -- don't do this or otherwise the tridiagonal matrix will not be correct anymore.

const LaVectorDouble& LaTridiagMatDouble::diag ( int  diag_selection  )  const

Returns the diagonal diag_selection: 0 main, -1 lower, 1 upper, 2 second upper.

(Actually, this class additionally stores the second upper diagonal of length N-2, selected by diag_selection==2, but this is only being used in LaTridiagMatFactorize().)

Note:
When assigning values or vectors to the returned diagonals, make sure you only use LaVectorDouble::inject instead of LaVectorDouble::copy or LaVectorDouble::operator=(). Please write this as follows: 
  LaVectorDouble newdiag(N);
  newdiag(0) = ...;
  LaTriagMatDouble triagmat(N);
  triagmat.diag(0).inject(newdiag); // correct
  // but don't write this:
  triagmat.diag(0) = newdiag; // wrong!

LaTridiagMatDouble& LaTridiagMatDouble::copy ( const LaTridiagMatDouble &  s  ) 

Release left-hand side (reclaiming memory space if possible) and copy elements of elements of s. Unline inject(), it does not require conformity, and previous references of left-hand side are unaffected.

LaTridiagMatDouble& LaTridiagMatDouble::inject ( const LaTridiagMatDouble &  s  ) 

Copy elements of s into the memory space referenced by the left-hand side, without first releasing it. The effect is that if other matrices share memory with left-hand side, they too will be affected. Note that the size of s must be the same as that of the left-hand side matrix.

Note:
If you rather wanted to create a new copy of s, you should use copy() instead.

LaTridiagMatDouble & LaTridiagMatDouble::ref ( LaTridiagMatDouble &   )  [inline]

Let this matrix reference the given matrix s, so that the given matrix memory s is now referenced by multiple objects (by the given object s and now also by this object). Handle this with care!

This function releases any previously referenced memory of this object.

const LaTridiagMatDouble& LaTridiagMatDouble::info (  )  const [inline]

use as in

std::cout << B.info() << std::endl;

this *info_ member is unique in that it really isn't part of the matrix info, just a flag as to how to print it. We've included in this beta release as part of our testing, but we do not expect it to be user accessable.

int LaTridiagMatDouble::debug (  )  const [inline]

Returns global debug flag

Friends And Related Function Documentation

std::ostream& operator<< ( std::ostream &  ,
const LaTridiagMatDouble &   
) [friend]

Print the matrix to the given output stream. If the matrix info flag is set, then this prints only the matrix info, see LaGenMatDouble::info(). Otherwise all matrix elements are printed.

The printing format of this NxN tridiagonal matrix is as follows: First the N-1 elements of the superdiagonal are printed, then the N elements of the diagonal, then the N-1 elements of the subdiagonal.

Generated on Sat Jul 14 11:40:37 2007 for Lapack++ by  doxygen 1.5.0