| void LaSymmBandMatFactorizeIP | ( | LaSymmBandMatDouble & | A | ) |
Factorize a real-valued symmetric positive definite band matrix with Cholesky factorization, in-place.
- Parameters:
-
A On entry, a real-valued symmetric positive definite band matrix A of dimension N x N. On exit, the lower triangular Cholesky factorization B with 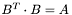
 1.5.0
1.5.0